4. Algebra de Boole, la base del lenguaje del PLC

                                                       Imagen generada por ChatGPT

Introducción a la programación de PLC: Álgebra de Boole

Índice

1. Introducción general.
2. ¿Cómo se comunica un PLC? Tipos de software.
3. Lenguajes de programación de PLC.
4. Álgebra de Boole aplicada a la automatización.
5. Puertas lógicas.
6. Ejercicios 
7. Conclusión

1. 🧭 Introducción general

En esta entrada exploraremos los fundamentos esenciales de los PLC, una habilidad clave en la automatización industrial moderna. Desde la estructura del software de un PLC hasta la lógica binaria basada en el Álgebra de Boole, te guiaré paso a paso por los conocimientos necesarios para comenzar a desarrollar programas lógicos de forma clara, precisa y estandarizada.

✅ Este contenido está diseñado para personas que están comenzando su formación como programadores de PLC, técnicos de automatización o entusiastas que buscan comprender cómo las máquinas “piensan” y toman decisiones a partir de entradas digitales.

2. ¿Cómo se comunica un PLC?

Programa de aplicación del usuario (Software de usuario)

Es el programa creado por el usuario para automatizar una tarea específica. Está compuesto por las instrucciones que definen la lógica de control del proceso y se escribe en el lenguaje de programación más conveniente para el programador.

Programa del sistema (Software interno)

Es el software interno del PLC, desarrollado por el fabricante. Su función es proporcionar servicios fundamentales al programa de usuario, como por ejemplo gestionar las entradas y salidas, almacenar la información, etc.

3. Lenguajes de programación de PLC

Durante mucho tiempo, cada fabricante diseñó su propio lenguaje, lo que dificultaba la portabilidad entre marcas. Para solucionar esto, se creó la norma IEC 61131-3, que estandariza los lenguajes de programación de PLC.

Los lenguajes estandarizados son:

• LD (Ladder Diagram) – Diagrama de contactos 
• FBD (Function Block Diagram) – Plano de funciones 
• ST (Structured Text) – Texto estructurado 
• IL (Instruction List) – Lista de instrucciones 
• SFC (Sequential Function Chart) / GRAFCET – Diagrama secuencial 

📌 En esta entrada no vamos a profundizar en los lenguajes de programación, eso lo haré más adelante profundizando el contenido en los más utilizados hoy en día LD y ST.

4. Álgebra de Boole aplicada a la automatización

¿Quién fue George Boole?

George Boole (1815–1864) fue un matemático y lógico inglés, considerado el padre de la lógica binaria. A pesar de no tener formación académica formal, desarrolló un sistema lógico basado en valores binarios (1 y 0) para describir operaciones del pensamiento humano.

En 1854, publicó su obra "An Investigation of the Laws of Thought", donde sentó las bases del Álgebra de Boole, la cual más tarde sería fundamental para la electrónica digital y la informática.

🧠 Su legado:

• Permitió crear circuitos electrónicos digitales.
• Su lógica es el lenguaje base de los microprocesadores, ordenadores y PLC.

Boole fue el primero en convertir la lógica en matemáticas. Antes de él, la lógica era filosófica, basada en palabras. Él propuso una forma de usar símbolos matemáticos (0 y 1) para representar valores de verdad (falso y verdadero) y operar con ellos como con números.

El comportamiento de los contactos eléctricos puede representarse mediante valores binarios:

• Contacto abierto = 0 (no permite paso de corriente).
• Contacto cerrado = 1 (permite paso de corriente).

¿Qué quiere decir esto? En nuestro día a día usamos los números del 0 al 9, combinándolos entre sí para expresar cifras más grandes (10, 125, 1000, etc.) pero en electricidad solo se puede saber si hay electricidad o no, 0 y 1, es decir la bombilla está encendida? 1 pero si esta apagada equivale a 0. Estos valores son la base sobre la que se construyen las operaciones lógicas.

4.1 Puertas lógicas

Las puertas lógicas son los bloques básicos del álgebra de Boole, esenciales para la programación de autómatas en lenguajes como el Plano de Funciones (FBD) o el Diagrama de Contactos (LAD). Estas funciones permiten modelar el comportamiento lógico de los automatismos y son la base de cualquier circuito de control.

Fuente: Curso Superior Autómatas Programables: UCAM

A continuación explicaremos cada una con un ejemplo, si es la primera vez que tratas este tema puede ser algo difícil de entender, por eso, más abajo te dejo unos videos donde lo explican más a fondo.

Puerta OR (Suma lógica)

📌 Símbolo lógico: F = A + B
🧠 Descripción: La salida será 1 si al menos una entrada es 1.

Ejemplo práctico: Imagina una máquina que puede arrancarse desde dos pulsadores distintos (A y B), uno ubicado en la entrada de la planta y otro junto al operario en el puesto de trabajo.

• Si ninguno de los pulsadores está pulsado (0 y 0), la máquina no se enciende.
• Si se pulsa uno de los dos (1 y 0 o 0 y 1), la máquina se enciende.
• Se si pulsan ambos, también se enciende.

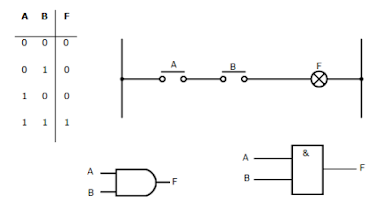
Puerta AND (multiplicación lógica)

📌 Símbolo lógico: F = A · B
🧠 Descripción: La salida es 1 sólo si todas las entradas son 1.

Ejemplo práctico: Para arrancar un motor es necesario que:

📍 Variables:
Pulsador_A: El pulsador de seguridad debe estar activo (1).
Pulsador_B: El pulsador de marcha debe estar activo (1).

🧠 Objetivo lógico:
Si uno de los dos no está activo, el motor no puede arrancar.

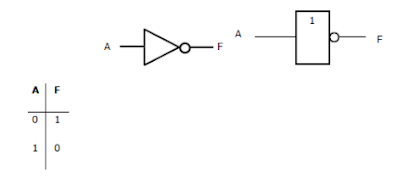
Puerta NOT (Inversión lógica) 

📌 Símbolo lógico: F = Ā

🧠 Descripción: Invierte el valor de entrada.

Ejemplo práctico: Un ventilador de extracción debe funcionar cuando NO hay una tapa en el sensor.

📍 Variables:
Sensor_1: Cuando detecta presencia el sistema no puede iniciar.

🧠 Objetivo lógico:
El ventilador debe encenderse cuando la tapa NO está presente.

Puerta NOR (NOT + OR)

📌 Símbolo lógico: F = ¬(A + B)
🧠 Descripción: La salida es 1 solo si todas las entradas son 0.

Ejemplo práctico: Un sistema de encendido por inactividad. Imagina una zona de trabajo peligrosa donde si detecta presencia no se activa, solamente trabajará cuando no detecte a nadie.

📍 Variables:

Sensor_1: Cuando detecta presencia el sistema no puede iniciar.

Sensor_2: Cuando detecta presencia el sistema no puede iniciar.

🧠 Objetivo lógico:

El sistema empieza a trabajar cuando no detecta a nadie en el entorno, es decir cuando los sensores indican (0).

Puerta NAND (NOT + AND)

📌 Símbolo lógico: F = ¬(A · B)
🧠 Descripción: La salida es 1 si al menos una entrada es 0

Ejemplo práctico: Una máquina de corte industrial debe detenerse automáticamente si ambas condiciones de riesgo están activadas al mismo tiempo.

📍 Variables:

Sensor_Tapa: Cuando no detecta la tapa cerrada es 0

Sensor Temperatura: Si la temperatura aumenta por encima de lo establecido es 0

🧠 Objetivo lógico:

Si una de las entradas es 1 o incluso las 2, la máquina se para o no puede encenderse hasta que sea seguro. 

Puerta XOR

🔺 Puerta XOR (O Exclusiva) 🔁

📌 Símbolo lógico: F = A·¬B + ¬A·B

🧠 Descripción: La salida es 1 solo si las entradas son diferentes.

Ejemplo práctico: Control de una lámpara desde dos pulsadores (conmutada).

📍 Variables:

Pulsador_1: En la planta alta

Pulsador_2: En la planta baja

🧠 Objetivo lógico:

Cada pulsación invierte el estado de la luz.

Puerta XNOR

🔻 Puerta XNOR (O Exclusiva Negada) 🔄
📌 Símbolo lógico: F = ¬(A ⊕ B)
🧠 Descripción: La salida es 1 si las entradas son iguales.

Ejemplo práctico: Dos compuertas que deben estar cerradas al mismo tiempo para permitir el paso de un producto o iniciar una operación.

📍 Variables:

Sensor_1: En la entrada

Sensor_2: En la salida

🧠 Objetivo lógico:

Se activa el transportador solo cuando ambos sensores indican el mismo estado (ambos abiertos o ambos cerrados).

Como has podido ver, las puertas lógicas tienen una función esencial, para profundizar más en el tema voy a dejar unos videos para darle un enfoque más práctico! ⬇️⬇️⬇️

¡¡Y unos ejercicios para practicar!!

7. Conclusión

El dominio del Álgebra de Boole y el entendimiento profundo de las puertas lógicas no solo forman la base de la programación de PLC, sino que representan el lenguaje con el que las máquinas modernas "piensan" y toman decisiones. Esta lógica binaria, heredada de los trabajos pioneros de George Boole, se ha convertido en el motor que impulsa la automatización industrial, desde simples controles hasta complejos sistemas inteligentes.

Te ánimo a profundizar en el temario en la bibliografía que te dejo abajo.

— Juanjo

Bibliografía

Álgebra de Boole. (n.d.). Wikipedia. Retrieved June 12, 2025, from https://es.wikipedia.org/wiki/%C3%81lgebra_de_Boole

Boole, G., Boole, J., & Parsons, R. (n.d.). George Boole. Wikipedia. Retrieved June 12, 2025, from https://es.wikipedia.org/wiki/George_Boole

Compuertas Lógicas: AND, OR , NOT , NAND, NOR y XOR 74LS - UNIT. (n.d.). UNIT Electronics. Retrieved June 12, 2025, from https://blog.uelectronics.com/electronica/circuitos-integrados-compuertas-logicas-and-or-nand-xor-y-not/

Descargar norma IEC 61131-3 gratis. (n.d.). Instrumcontrol. Retrieved June 12, 2025, from https://instrumcontrol.com/descargar-norma-iec-61131-3-gratis/

Introducción al estándar IEC 61131-3. (n.d.). Instrumentacion y Control NET. Retrieved June 12, 2025, from https://instrumentacionycontrol.net/wp-content/uploads/2017/11/IyCnet_Intro_estandar_IEC_61131-3.pdf

Puertas lógicas: qué son y para que sirven. (2022, September 25). Profesional Review. Retrieved June 12, 2025, from https://www.profesionalreview.com/2022/09/25/puertas-logicas/

Estructura y diseño ChatGPT